科学計算ライブラリ「numpy」を用いて、waveファイルの情報から高速フーリエ変換(FFT)による周波数解析を行います。C#でのFFTは既に「C#によるWaveデータのFFT処理」で行いました。今回は「SPH0645LM4H搭載 I2S MEMSマイクを使ってRaspberry Pi 3で録音」で録音したwaveファイルを用いて、pythonの科学計算ライブラリ「numpy」を使用します。
周波数解析プログラムの作成
周波数解析プログラム「fftmodule.py」を次に示します。
- 28行目で1フレーム4バイトのため、「dtype= “int32″」として、-1~1に正規化します。
- 32行目で高速フーリエ変換を行います。
- 35行目で周波数解析した周波数リストを取得します。
- 39-43行目で波形サンプル画面を描画します。
- 46-50行目で振幅スペクトルを描画します。
fftmodule.py
# -*- coding: utf-8 -*-
import wave
import numpy as np
import matplotlib.pyplot as plt
def main():
filename = "mic500hz.wav"
wf = wave.open(filename, "r" )
# WAVファイルの情報を表示
print ("オーディオチャンネル数(モノラル: 1 ステレオ:2 ) : ", wf.getnchannels())
print ("サンプルサイズ(バイト数) : ", wf.getsampwidth())
print ("サンプリングレート : ", wf.getframerate())
print ("オーディオフレーム数 : ", wf.getnframes())
print ("圧縮形式 : ", wf.getcomptype())
print ("(圧縮形式) : ", wf.getcompname())
print ("パラメータ : ", wf.getparams())
print ("記録時間(Sec) : ", float(wf.getnframes()) / wf.getframerate() )
fs = wf.getframerate() # サンプリング周波数
g = wf.readframes(wf.getnframes())
print('00: {:X} {:X} {:X} {:X} {:X} {:X} {:X} {:X} - {:X} {:X} {:X} {:X} {:X} {:X} {:X} {:X}\n'.
format(g[0],g[1],g[2],g[3],g[4],g[5],g[6],g[7],g[8],g[9],g[10],g[11],g[12],g[13],g[14],g[15]))
print('10: {:X} {:X} {:X} {:X} {:X} {:X} {:X} {:X} - {:X} {:X} {:X} {:X} {:X} {:X} {:X} {:X}\n'.
format(g[16],g[17],g[18],g[19],g[20],g[21],g[22],g[23],g[24],g[25],g[26],g[27],g[28],g[29],g[30],g[31]))
print('10: {:X} {:X} {:X} {:X} {:X} {:X} {:X} {:X} - {:X} {:X} {:X} {:X} {:X} {:X} {:X} {:X}\n'.
format(g[32],g[33],g[34],g[35],g[36],g[37],g[38],g[39],g[40],g[41],g[42],g[43],g[44],g[45],g[46],g[47]))
g = np.frombuffer(g, dtype= "int32")/2147483648.0 # -1~1に正規化
wf.close()
n0 = 168912 # サンプリング開始位置
N = 4096 # サンプル数
G = np.fft.fft(g[n0:n0+N]) # 高速フーリエ変換
amp = [np.sqrt(c.real ** 2 + c.imag ** 2) for c in G] # 振幅スペクトル
phase = [np.arctan2(int(c.imag), int(c.real)) for c in G] # 位相スペクトル
flist = np.fft.fftfreq(N, d=1.0/fs) # 周波数リスト
# 波形サンプルを描画
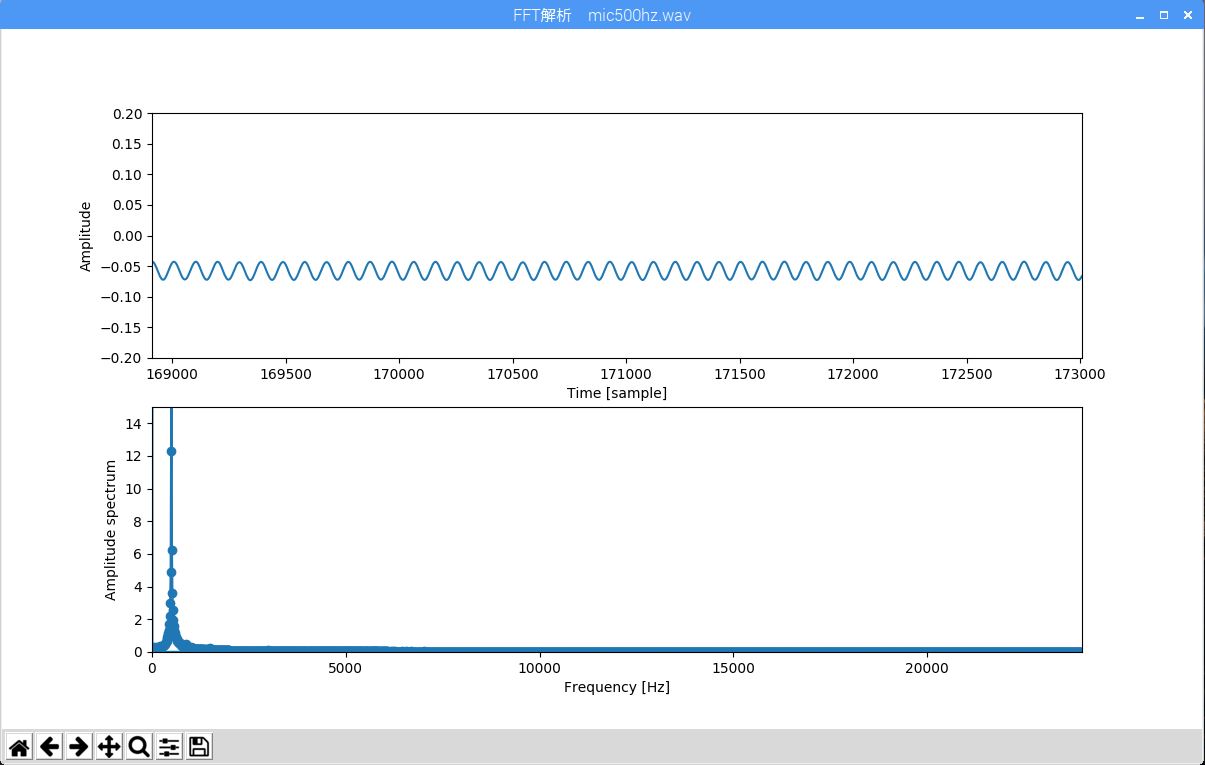
plt.figure("FFT解析 "+filename,figsize=(12,7))
plt.subplot(211)
plt.plot(range(n0, n0+N), g[n0:n0+N])
plt.axis([n0, n0+N, -0.2, 0.2])
plt.xlabel("Time [sample]")
plt.ylabel("Amplitude")
# 振幅スペクトルを描画
plt.subplot(212)
plt.plot(flist, amp, marker='o', linestyle='-')
plt.axis([0, fs/2, 0, 15])
plt.xlabel("Frequency [Hz]")
plt.ylabel("Amplitude spectrum")
plt.show()
if __name__ == '__main__':
main()
周波数解析プログラムの実行
作成した周波数解析プログラム「fftmodule.py」を次のコマンドで実行します。
$ python3 fftmodule.py オーディオチャンネル数(モノラル: 1 ステレオ:2 ) : 1 サンプルサイズ(バイト数) : 4 サンプリングレート : 48000 オーディオフレーム数 : 479232 圧縮形式 : NONE (圧縮形式) : not compressed パラメータ : _wave_params(nchannels=1, sampwidth=4, framerate=48000, nframes=479232, comptype='NONE', compname='not compressed') 記録時間(Sec) : 9.984 00: 0 0 0 0 0 0 0 0 - 0 0 0 0 0 0 0 0 10: 0 0 0 0 0 80 61 B - 0 0 5 E7 0 80 2 FA 10: 0 80 2 FA 0 C0 2 FA - 0 C0 5 FA 0 0 9 FA
画面に表示された周波数解析結果を次に示します。
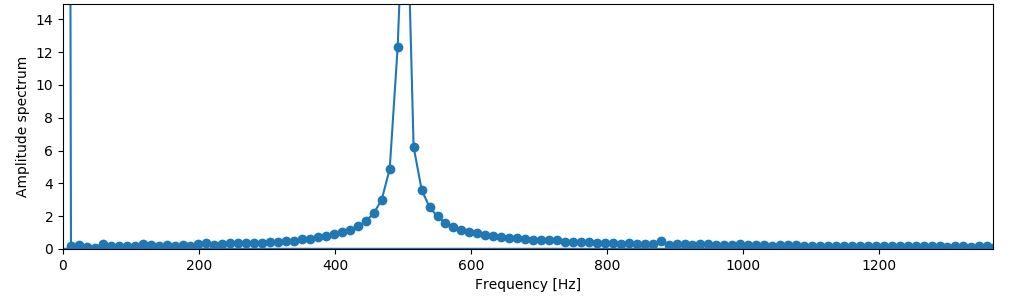
周波数解析結果の500Hz近辺を拡大表示します。