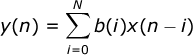Python言語を使って、FIRディジタルフィルタを作成します。入力・出力ともwavファイルとします。
FIRディジタルフィルタとは
ディジタルフィルタは、次の3つの要素の組み合わせによって構成されます。
- 乗算器
- 加算器
- 遅延器
この組み合わせ方によって、無限長の時間においてゼロでない値を返すインパルス応答関数を持つ無限インパルス応答 IIR)と、有限の時間についてのインパルス応答があるものを有限インパルス応答 (FIR) とに分けられます。
FIRフィルタの定義式は、次のように畳み込みの定義式と同じです。x(n)は入力信号、y(n)は出力信号、b(i)は乗算器のフィルタ係数、Nは遅延器の数(フィルタ係数の数はN+1)です。
実際にプログラム化するには次のように行います。
| 乗算器のフィルタ係数 | 入力信号 | 処理 |
|---|---|---|
| b(0) | x(n) | 入力信号x(n)にフィルタ係数b(0)を乗算 |
| b(1) | x(n-1) | 入力信号x(n-1)にフィルタ係数b(1)を乗算 |
| b(2) | x(n-2) | 入力信号x(n-2)にフィルタ係数b(2)を乗算 |
| ・・・ | ・・・ | ・・・ |
| b(N) | x(n-N) | 入力信号x(n-N)にフィルタ係数b(N)を乗算 |
これらを加算した値が出力信号値y(n)になります。
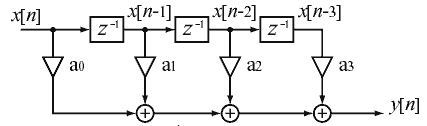
乗算器等は次のように構成され、『ある定数』との乗算を行ってから足しあわせます。次に示すa0,a1,a2,…の定数や、遅延器の数を変えることにより、ローパス、ハイパス、バンドパスなど様々なフィルタを実現できます。
FIRディジタルフィルタスクリプトの作成
Python言語を使ってFIRディジタルフィルタスクリプトを作成します。「wavファイルの作成とwavファイル情報の表示」で作成したwavファイルを入力します。ただし、記録時間は30秒から3秒にしました。
- load_wave関数はwavファイルの読み込みです。
- save_wave関数はwavファイルの書き込みです。
- makeCoefficient関数はフィルタ係数の作成です。
- main関数から起動されます。
firtest.py
# -*- coding: utf-8 -*-
import wave
import numpy as np
import matplotlib.pyplot as plt
import struct
import csv
# waveファイルの読み込み
def load_wave(filename):
wr = wave.open(filename, "rb")
fs = wr.getframerate()
rdata = wr.readframes(wr.getnframes())
data = np.frombuffer(rdata, dtype="int16")/32768.0
return data, fs
# waveファイルへ保存
def save_wave(data, bit, fs, filename):
maxvalue = np.max(np.abs(data))
# print (maxvalue)
g = [int(v/maxvalue * 32767.0) for v in data]
g = struct.pack("h" * len(g), *g)
wf = wave.open(filename, "w")
wf.setnchannels(1)
wf.setsampwidth(bit)
wf.setframerate(fs)
wf.writeframes(g)
wf.close()
# フィルタ係数の作成
def makeCoefficient():
arr = np.array( [] )
with open("constant") as f:
for row in f:
# print (row.strip())
arr = np.append(arr, float(row))
return arr
# FIRフィルタ(元信号, フィルタ係数)
def fir(g, b):
gf = [0.0] * len(g) # フィルタの出力信号
N = len(b) - 1 # フィルタ係数の数
for n in range(len(g)):
for i in range(N+1):
if n - i >= 0:
gf[n] += b[i] * g[n-i]
# print('b:{} g:{} '.format(b[i],g[n-i]))
# print('n:{} gf:{} '.format(n,gf[n]))
return gf
def main():
data, fs = load_wave("100-500-1000-8000hz.wav") # waveファイルの読み込み
b = makeCoefficient() # フィルタ係数の作成
firdata = fir(data, b) # FIRフィルタ処理
save_wave(firdata, 2, fs, "fir.wav")# 出力信号を保存
if __name__ == '__main__':
main()
makeCoefficient関数で読み込まれるファイル「constant」の内容を次に示します。この係数により高周波成分が減衰し、波形も滑らかになります。
0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1
FIRディジタルフィルタスクリプトの実行
次のコマンドで作成したFIRディジタルフィルタスクリプトを実行します。
$ python3 firtest.py
入力したwavファイル「100-500-1000-8000hz.wav」を次に示します。
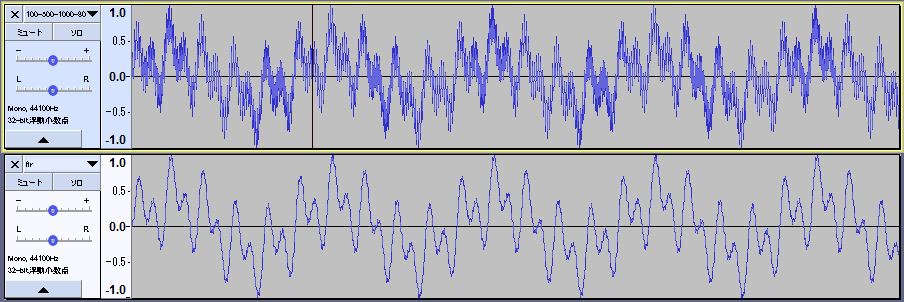
FIRディジタルフィルタ後のwavファイル「fir.wav」を次に示します。高周波成分が減衰したため高い音が小さくなり、低音が拡大されています。
audacityアプリを用いて、入力した波形「100-500-1000-8000hz.wav」(上側)とFIRディジタルフィルタ後の波形「fir.wav」(下側)を比較します。
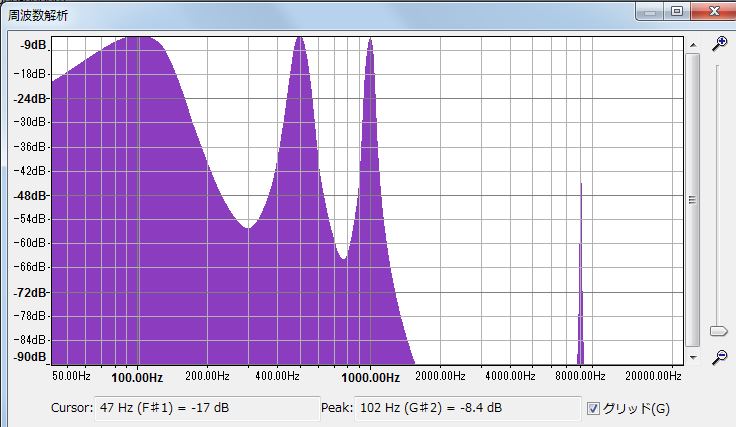
audacityアプリでFIRディジタルフィルタ後の波形をFFT処理すると、100、500、1000、8000hzのそれぞれが変わっていないことが確認できました。